In the real world sound is an analog wave. It has an infinite resolution and infinite detail – we can keep measuring in higher detail and extract more data.
On computers we don’t have infinite amounts of secondary storage space so we must create the best representation of sound that we can.
Here we have an analog sound wave. On the y axis we have amplitude. Amplitude is the volume or how loud the audio is. On the x axis we have the duration of the audio in seconds. This audio recording is 2 seconds long.
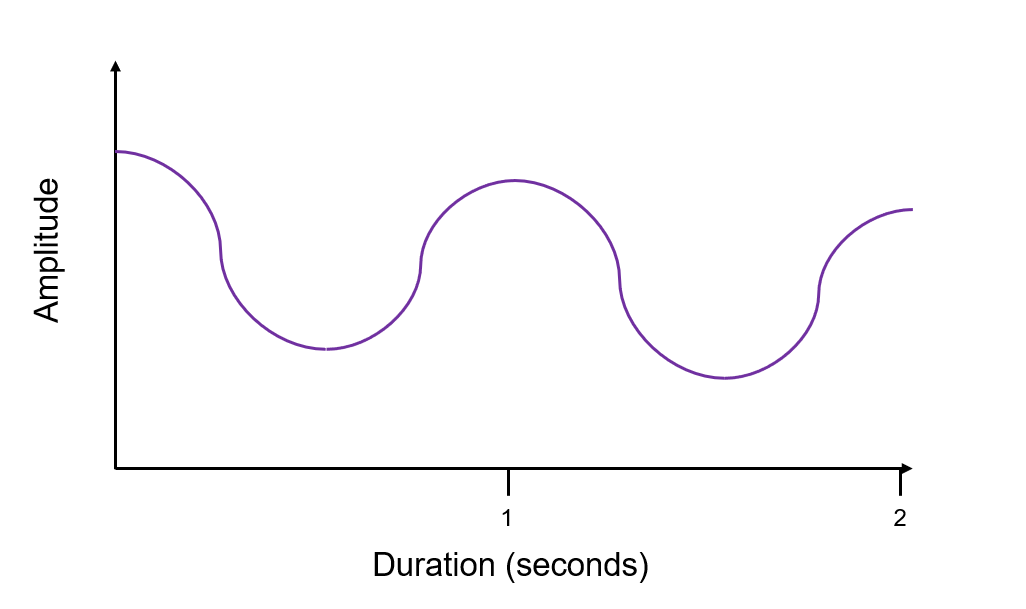
Analogue audio has an infinite resolution, so it’s impossible for a computer to process and store it. Because of this, digital audio breaks up the analogue signal into chunks, or ‘samples’.
Firstly we need to decide our bit depth. Bit depth is the resolution. In the example below we have a bit depth of 4, which means we can measure the amplitude on a scale of 0 to 15.
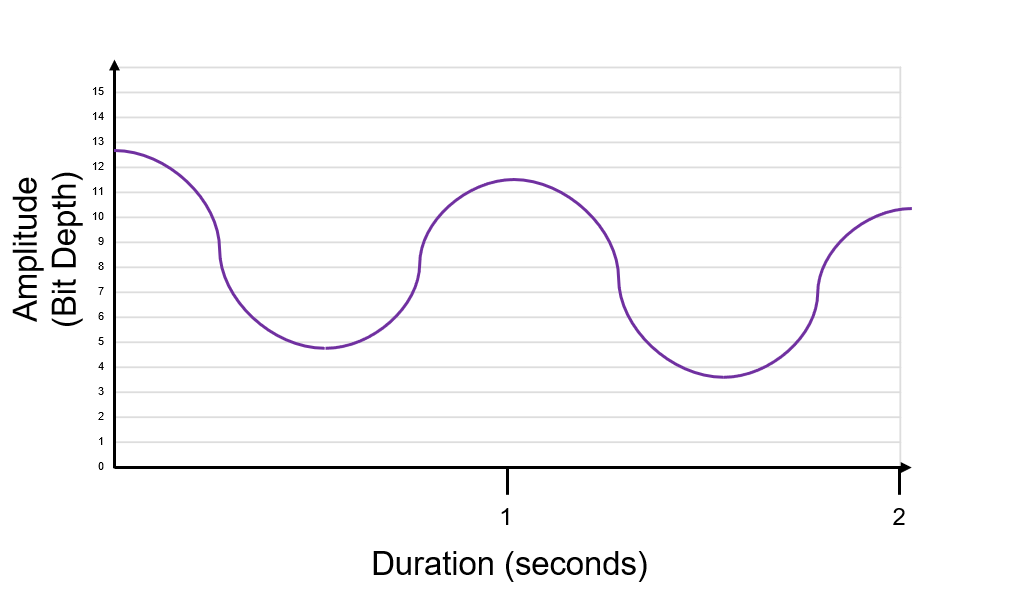
We then need to decide the sample rate. The sample rate is how many times we sample the analogue wave every second. Sample rate is measured in Hertz (Hz), samples per second, or more often Kilohertz (KHz), thousands of samples per seconds. The example sample rate below is 8Hz.
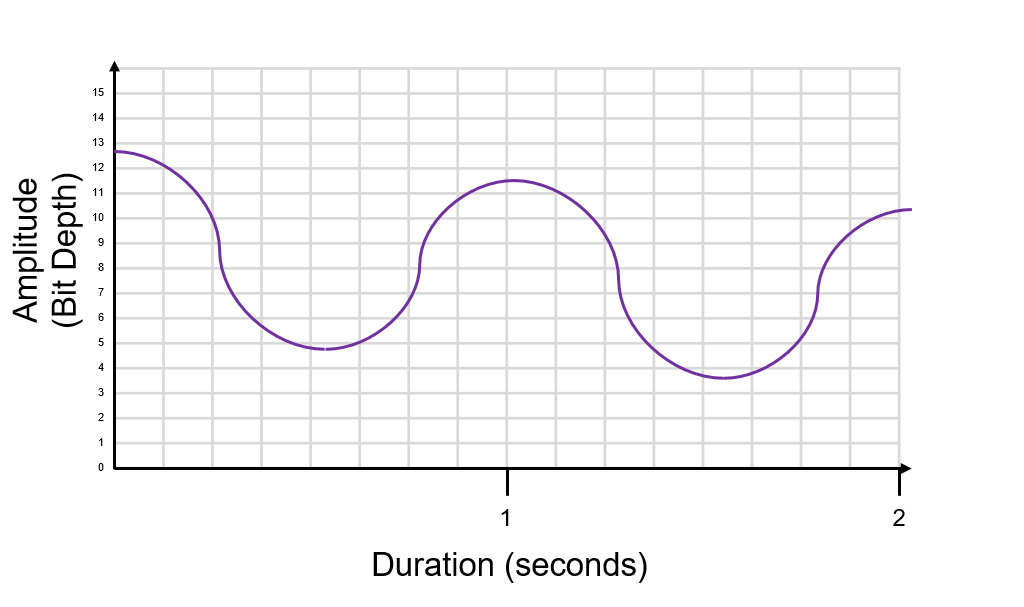
At every 1Hz we take our sample and plot it. We have to plot it against the bit depth (sample rate must cross with our 0-15 scale). Sometimes you will need to round up or down (nearest intersection).
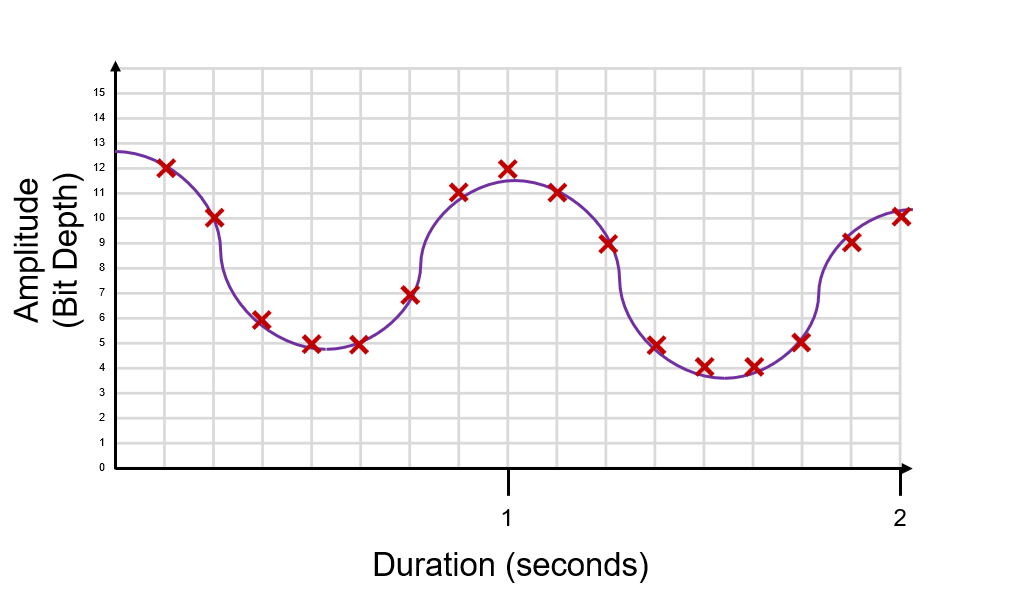
We draw in straight lines to show the digital digital signal. We “sample” (draw line vertically) and the hold (draw line horizontally to the next sample).
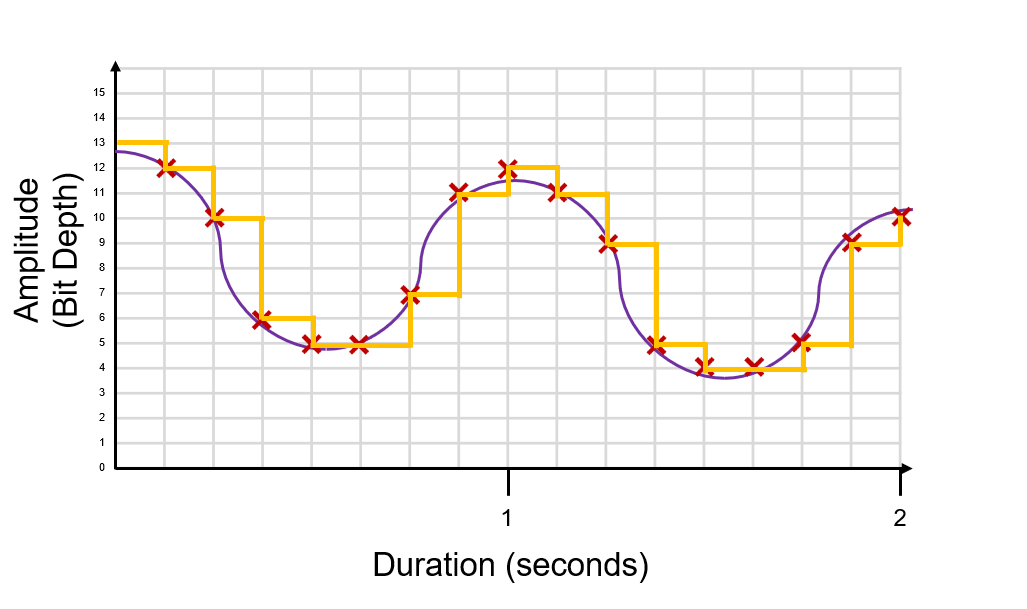
This is our digital signal that represents our original analogue sound wave.
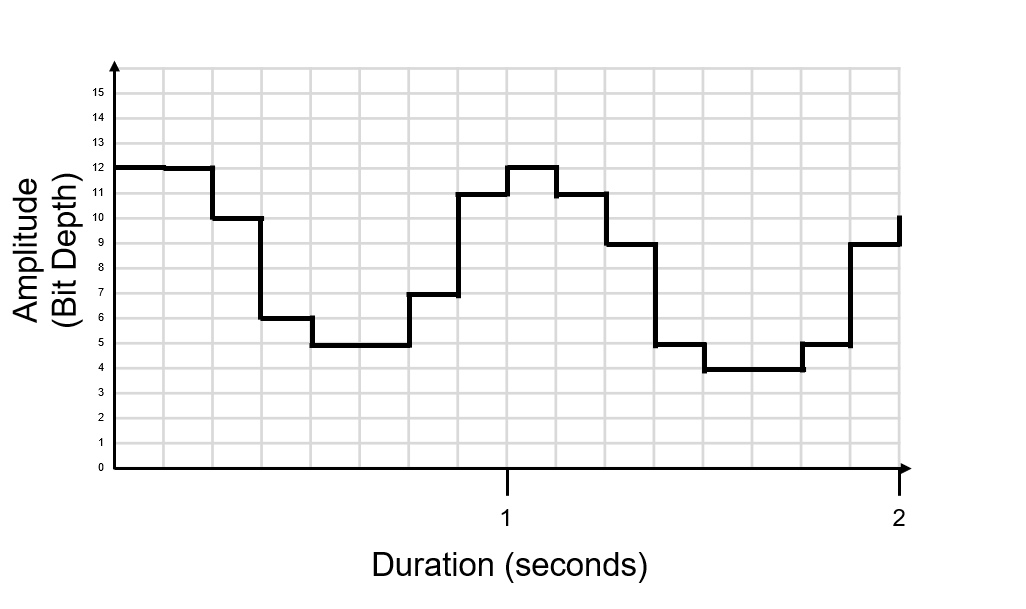
Because of this, digital audio is always an approximation of the original analogue audio, regardless of the bit depth and sample rate.
Bit depth is the number of bits we store each time we take a sample. The more bits we store per sample the higher the quality of the audio.
When storing more bits per sample we increase the size of the file.
The sample rate is how many times a second we take our sample. It is measured in Hz or KHz.
The more samples per second we take the higher the quality of the audio, however the larger the size of the audio file.
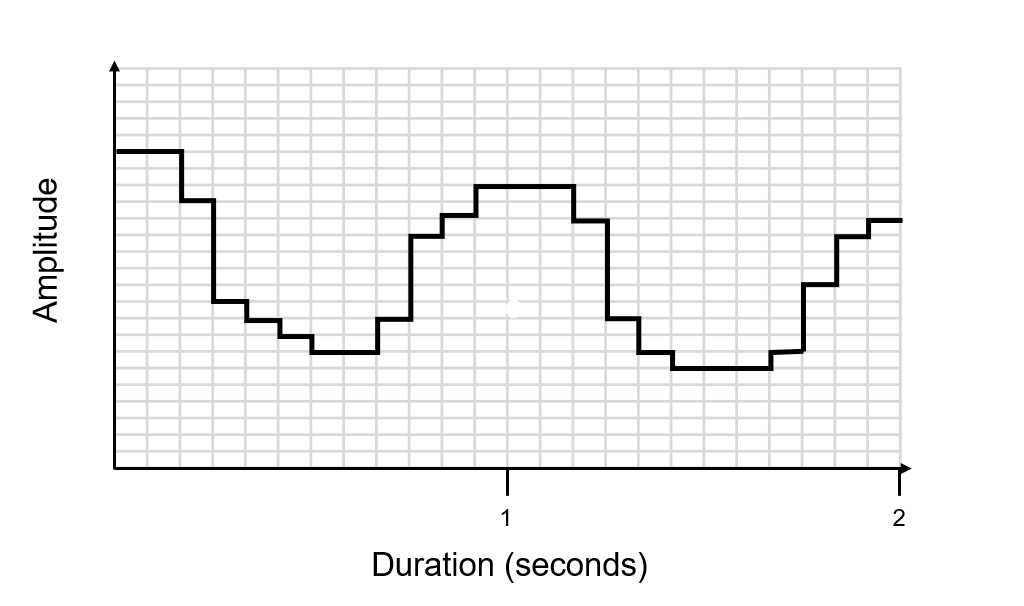
Increasing both bit depth and sample rate will create a digital signal closer to the analog sound wave, but never exactly the same. We aim to get the digital signal as close as possible to the analog sound wave.
Here is the original digital signal from the previous example:
This is the digital signal with a greater bit depth and a higher sample rate:
When calcualting the file size of a raw sound file we can simply take the number of bits stored per sampel (bit depth) and multiply it by the sample rate (hz) and the duration of the sound file (seconds). This is often done by using the following expression
bits = Sample Rate (Hz) x Bit Depth (bits) x Duration (seconds)
You may need to convert the bits to another unit and we can do this by dividing the number of bits. The table below shows you what you would need to divide by to get to the desired unit for both OCR and Edexcel GCSE Specification. Remember for each step down the table you have to carry out all of the division up to that point.
| Unit | Edexcel | OCR |
| Bit | - | - |
| Byte | /8 | /8 |
| Kibibyte / Kilobyte | /1024 | /1000 |
| Mebibyte / Megabyte | /1024 | /1000 |
| Gibibyte / Gigabyte | /1024 | /1000 |