Data Representation
Understand how computers represent images, sound, and characters in binary. Explore the fascinating methods of data representation that enable computers to process and display information.
A character is an individual letter, number or symbol Computers work entirely using binary math and logic, but need to be able to display written human languages (and their characters) – otherwise they wouldn’t be much use to us! Computers represent each characters we use with a unique binary number. A character set is the table a computer uses to convert the unique binary numbers into the characters that we use.
ASCII is a character set that was created in the 1960s in the US. ASCII is an acronym for the American Standard Code for Information Interchange. It was based on telegraph code and each character is represented by 7 bits. Using 7 bits means that ASCII can represent 128 characters (lowercase, uppercase, numbers, a range of symbols, and control characters). The order of characters in the ASCII character set follows a logical order: e.g. A (65 in denary) is followed by B (66 in denary) so it it possible to deduce the binary representation of characters if you have some reference.
Limitations of ASCII
With only using 7 bits, 128 characters can only cover characters within the English language. As more countries began to use computers and interest grew in being able to use them to communicate there became a need to represent a larger number of characters. ASCII Extended was created to make use of 8 bits. This allowed 256 characters to be used and included a range of additional Latin characters including those with accents.
Over time ASCII Extended became too limiting and we created a new character set called Unicode. All computers worldwide are capable of using the Unicode character set. Unicode can get quite complicated, but to keep it simple for the exam, we’ll say each character uses 16 bits and we can represent around 65,000 characters The first 256 characters in Unicode match those in ASCII and ASCII Extended to maintain backward compatibility.
Benefits of Unicode
- Contains a large number of the worlds symbols.
- Almost all devices can decode text sent to them using Unicode.
- Backwards compatible with ASCII (the first 128 characters use the same unique binary numbers!)
- Contains emoji
Everything in the real world is analog it has an infinite resolution limited only by the tools we use to measure it.
Everything on the computer is digital and we only have a finite amount of storage and memory.
When we want to store things from the real world on computers we cannot store all of this detail. We try our best to represent the real world on computers but it’s only a “sample” of what’s there in real life.
To store anything from the real world onto a computer we have to use a ADC (Analog to Digital Converter). When using a ADC we are taking these samples of the real world, and the digital quality of the data captured is dependent upon the resolution of the ADC.
Bitmap images are composed of tiny dots known as pixels, similar to a mosaic pattern. The majority of images, such as digital photographs, are bitmap images.
Digital photos function by sampling the real world, capturing its details in digital format. Bitmap images possess finite quality, which means it is not possible to continually zoom into them while retaining quality.
When capturing the real world in a bitmap image, the amount of data recorded and stored significantly influences the quality of the image.
Factors that affect the file size and quality of an image include:
- Width - measured in pixels
- Height - measured in pixels
- Colour depth - measured in bits
Colour Depth
Each pixel in a bitmapimage is represented by a binary number. The number of individual bits affects how many possible colours can be shown, where the unique combinations of bits is the number of colours that can be represented.
If an image which stores 1 bit per pixel and only show 2 colours, with there being 2 possible values that can be stored with 1 bit (1 or 0).
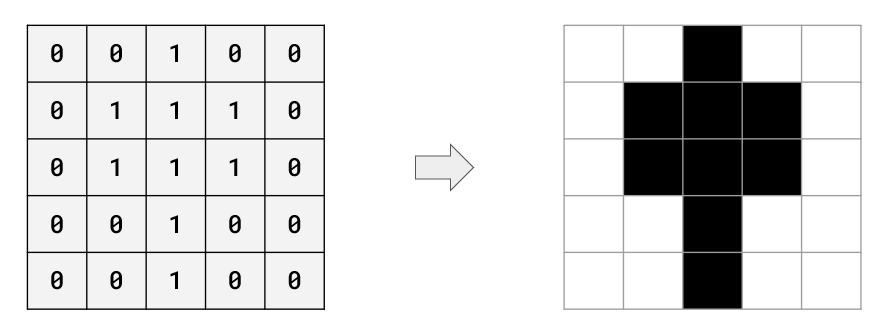
If we double the number of bits stored per pixel (2 bits per pixel) we can now represent 4 different colours because there are 4 unique combinations we can make with 2 bits (00, 01, 10, 11)
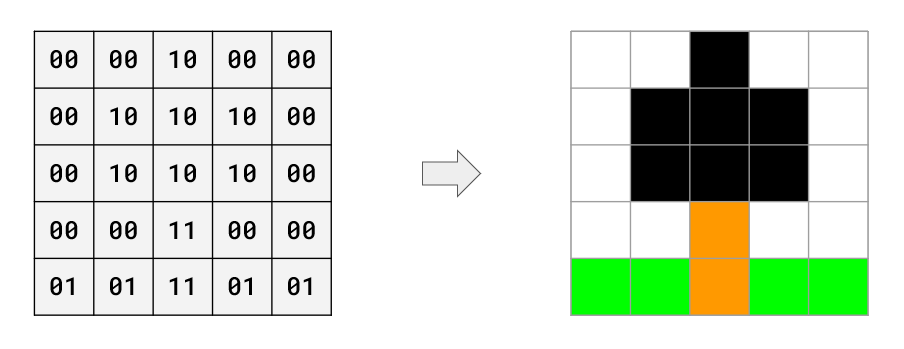
The more bits that we used to represent each pixel increases the number of colours we can represent, however this also increases the size of the bitmap image file. Using the above examples while the second image of a tree is more realistic due to the number of colours we can represent we have doubled the number of bits that it takes to store the image (25 bits vs 50 bits).
When storing a bitmap image the raw values for each pixel is stored as a continuous string. The above 2 bit example would be stored as the following:
00001000000010101000001010100000001100000101110101
Meta data would also be added such as width, height and colour depth to allow the computer to interpret the stream of binary digits to reproduce the image.
Calculating File Size
When calcualting the file size of a raw bitmap image we can simply take the number of bits stored per pixel (colour depth) and multiply it by the number of pixels that make up the image. This is often done by using the following expression
bits = width(px) x height (px) x colour depth (bits)
You may need to convert the bits to another unit and we can do this by dividing the number of bits. The table below shows you what you would need to divide by to get to the desired unit for both OCR and Edexcel GCSE Specification. Remember for each step down the table you have to carry out all of the division up to that point.
| Unit | Edexcel | OCR |
| Bit | - | - |
| Byte | /8 | /8 |
| Kibibyte / Kilobyte | /1024 | /1000 |
| Mebibyte / Megabyte | /1024 | /1000 |
| Gibibyte / Gigabyte | /1024 | /1000 |
For example, if you have an image which is 50px wide, 60px height and has a colour depth of 4 and we need the file size to be represented in Kibibytes / Kilobytes:
OCR
Bits - 50 x 60 x 4 = 12000 bits
Kilobytes - 12000 / 8 / 1000 = 1.5
Edexcel
Bits - 50 x 60 x 4 = 12000 bits
Kibibytes - 12000 / 8 / 1024 = 1.46
Remember on the Edexcel specification you do not need to carry out the expression.
Metadata
Metadata is a term used throughout computing and is not exclusive to images.
Metadata is additional data attached to a file to help describe itself (metadata literally means data about itself).
With images we need metadata to help construct the image by providing a width, height and colour depth. We can also store data on the camera model an image was taken with, data / time and the location a photo was taken.
Metadata does increase the file size of a bitmap image, however usually compared to the rest of the image this size increase is minimal
In the real world sound is an analog wave. It has an infinite resolution and infinite detail – we can keep measuring in higher detail and extract more data.
On computers we don’t have infinite amounts of secondary storage space so we must create the best representation of sound that we can.
Converting Analog Waves to Digital Waves
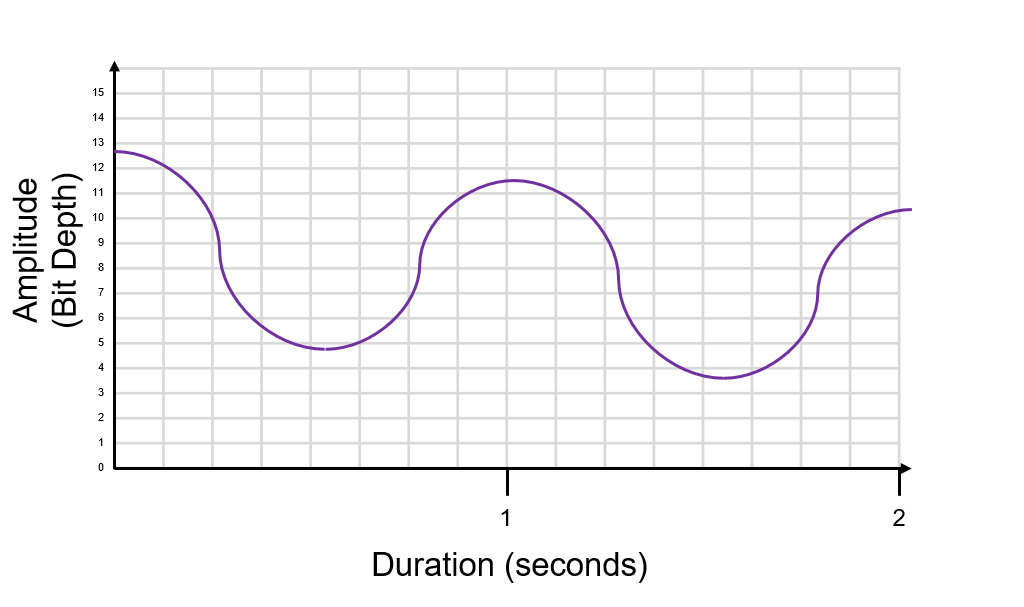
Here we have an analog sound wave. On the y axis we have amplitude. Amplitude is the volume or how loud the audio is. On the x axis we have the duration of the audio in seconds. This audio recording is 2 seconds long.
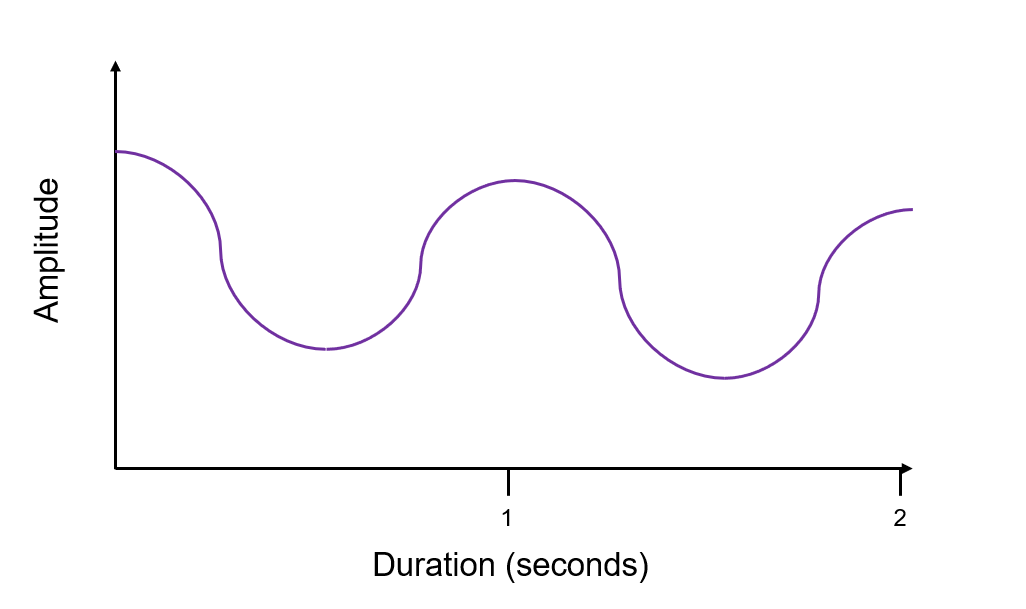
Analogue audio has an infinite resolution, so it’s impossible for a computer to process and store it. Because of this, digital audio breaks up the analogue signal into chunks, or ‘samples’.
Firstly we need to decide our bit depth. Bit depth is the resolution. In the example below we have a bit depth of 4, which means we can measure the amplitude on a scale of 0 to 15.
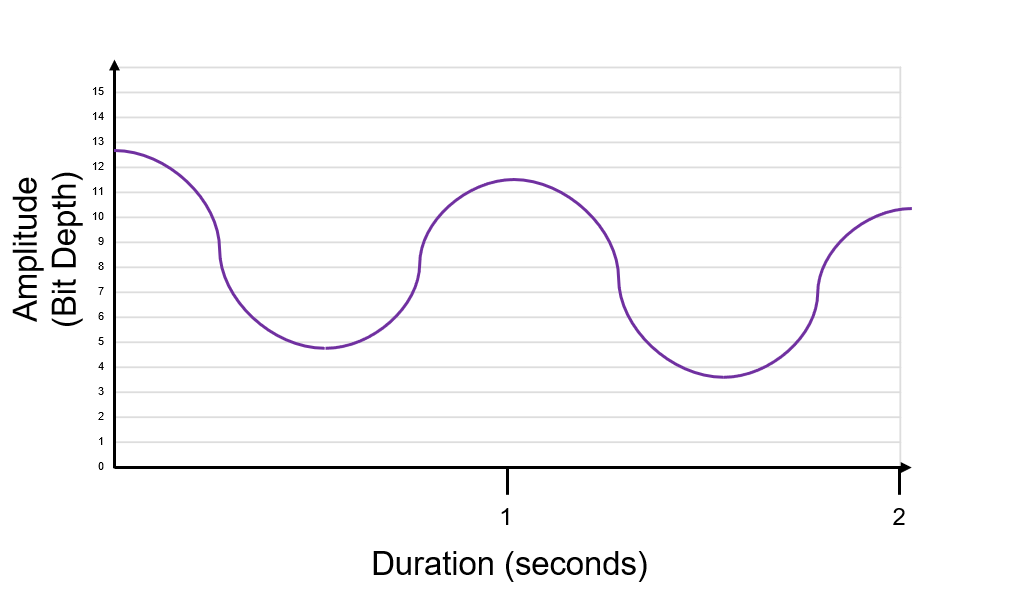
We then need to decide the sample rate. The sample rate is how many times we sample the analogue wave every second. Sample rate is measured in Hertz (Hz), samples per second, or more often Kilohertz (KHz), thousands of samples per seconds. The example sample rate below is 8Hz.
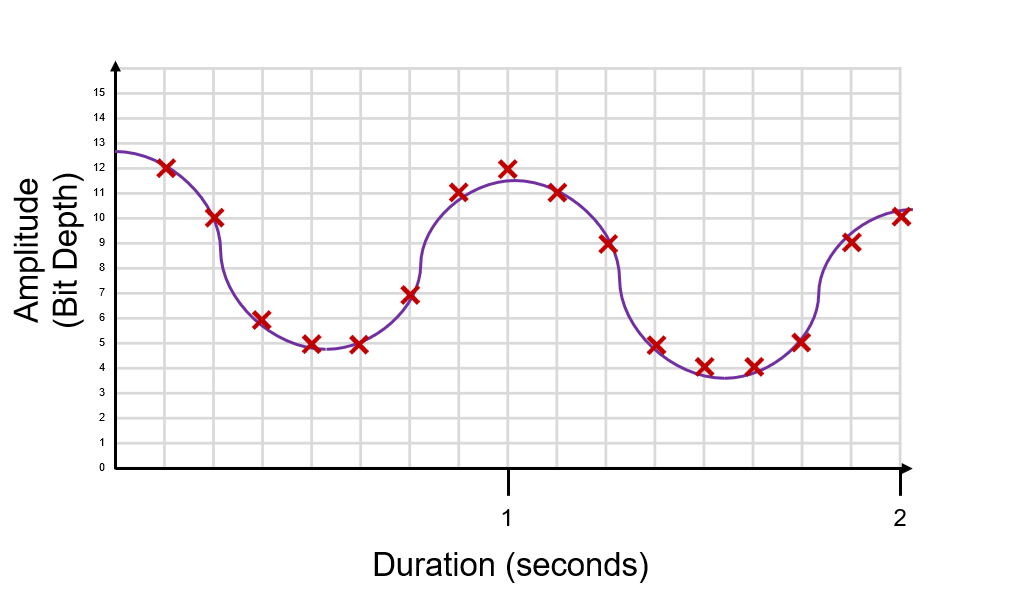
At every 1Hz we take our sample and plot it. We have to plot it against the bit depth (sample rate must cross with our 0-15 scale). Sometimes you will need to round up or down (nearest intersection).
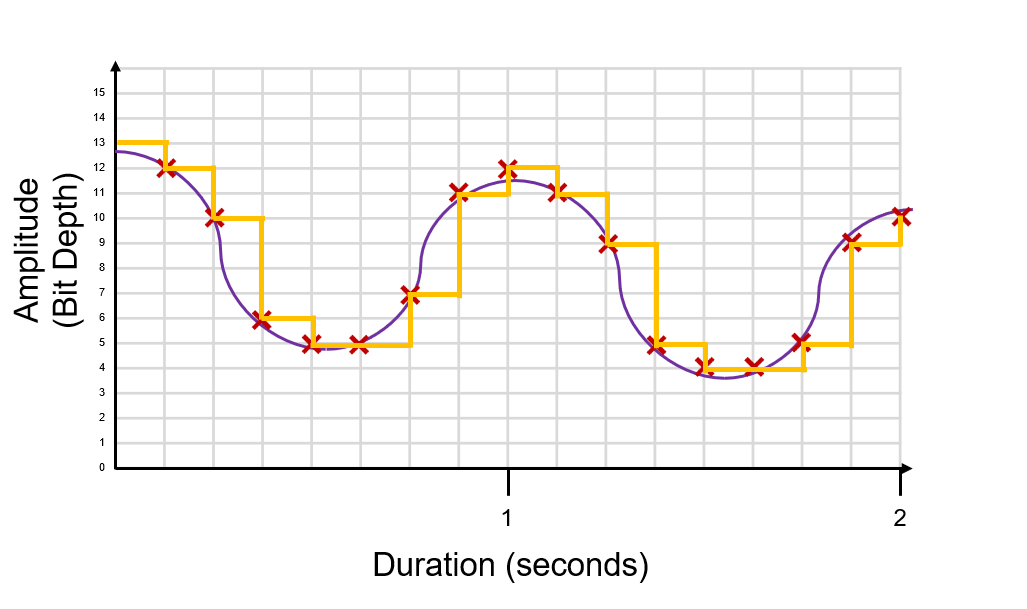
We draw in straight lines to show the digital digital signal. We “sample” (draw line vertically) and the hold (draw line horizontally to the next sample).
This is our digital signal that represents our original analogue sound wave.
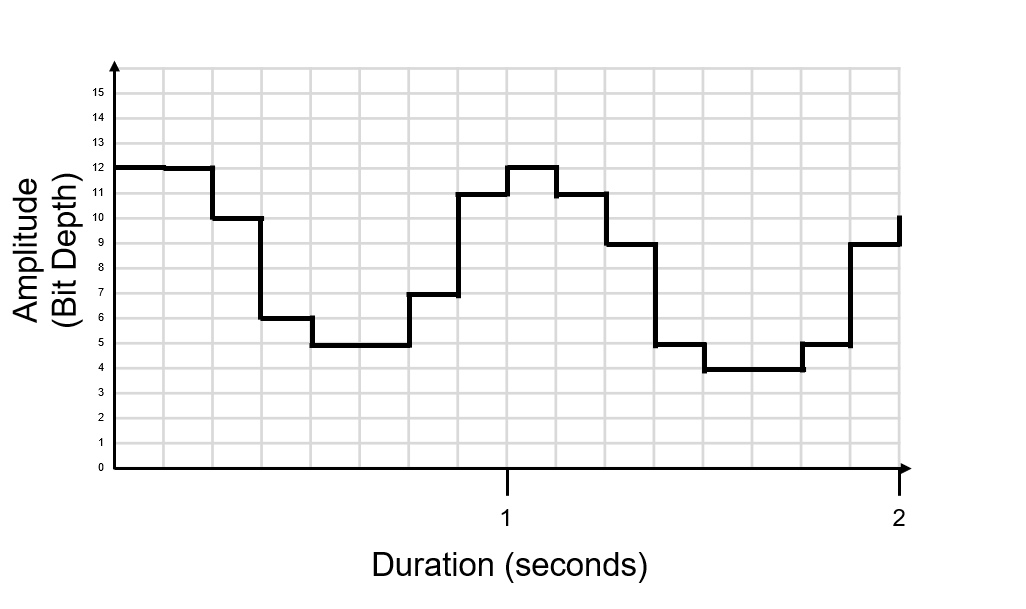
Because of this, digital audio is always an approximation of the original analogue audio, regardless of the bit depth and sample rate.
Bit Depth
Bit depth is the number of bits we store each time we take a sample. The more bits we store per sample the higher the quality of the audio.
When storing more bits per sample we increase the size of the file.
Sample Rate
The sample rate is how many times a second we take our sample. It is measured in Hz or KHz.
The more samples per second we take the higher the quality of the audio, however the larger the size of the audio file.
Quality
Increasing both bit depth and sample rate will create a digital signal closer to the analog sound wave, but never exactly the same. We aim to get the digital signal as close as possible to the analog sound wave.
Here is the original digital signal from the previous example:
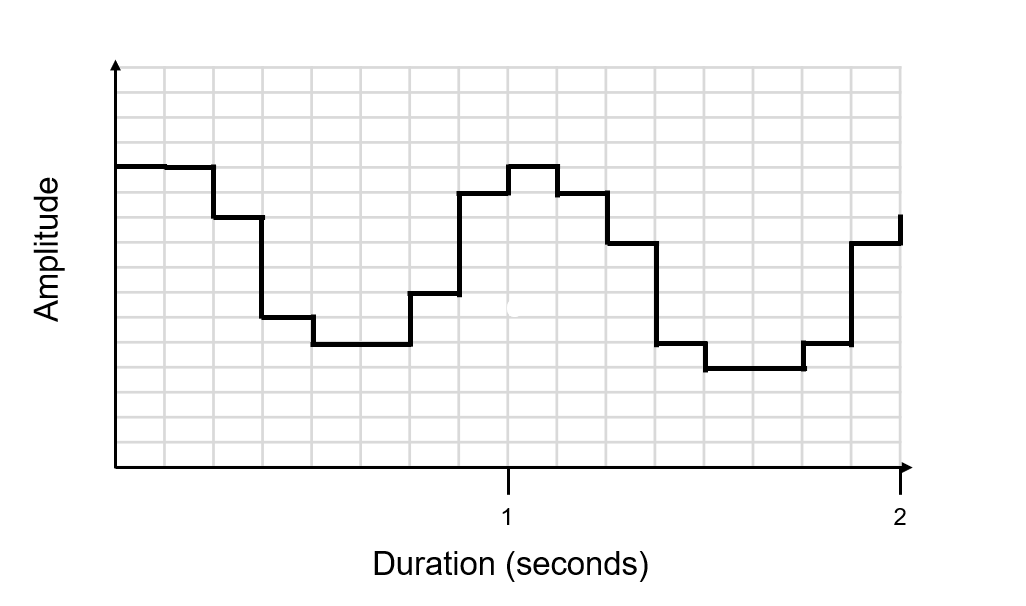
This is the digital signal with a greater bit depth and a higher sample rate:
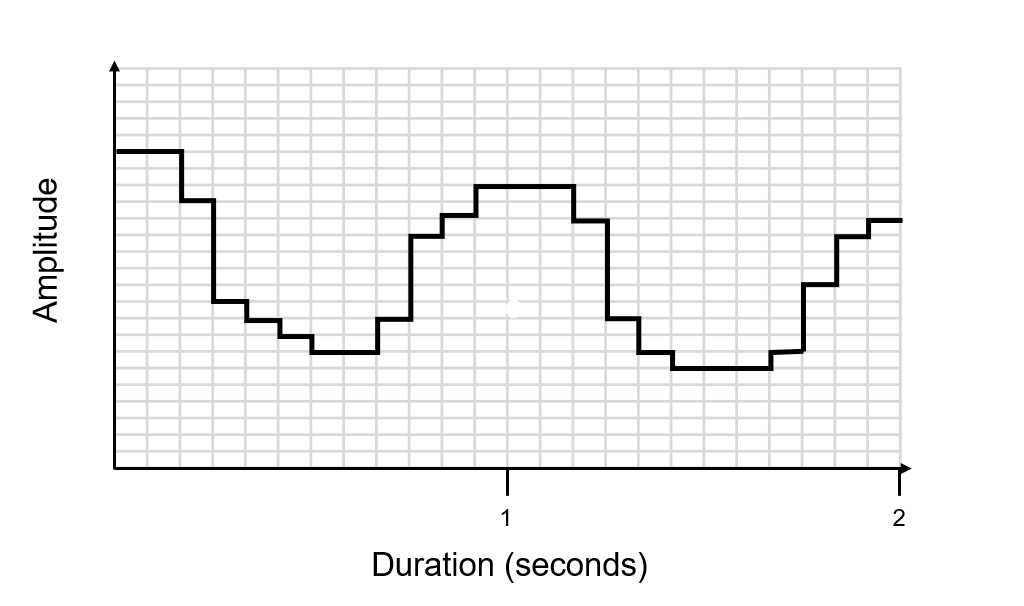
Calculating File Size
When calcualting the file size of a raw sound file we can simply take the number of bits stored per sampel (bit depth) and multiply it by the sample rate (hz) and the duration of the sound file (seconds). This is often done by using the following expression
bits = Sample Rate (Hz) x Bit Depth (bits) x Duration (seconds)
You may need to convert the bits to another unit and we can do this by dividing the number of bits. The table below shows you what you would need to divide by to get to the desired unit for both OCR and Edexcel GCSE Specification. Remember for each step down the table you have to carry out all of the division up to that point.
| Unit | Edexcel | OCR |
| Bit | - | - |
| Byte | /8 | /8 |
| Kibibyte / Kilobyte | /1024 | /1000 |
| Mebibyte / Megabyte | /1024 | /1000 |
| Gibibyte / Gigabyte | /1024 | /1000 |