CPUs are made up of billions of tiny switches. These switches can either be on or off and cannot work with the numbers we use (denary, 0-9) or our languages. Everything on a computer must be broken down to binary (0s and 1s). 0 = Off 1 = On Humans use denary numbers and It’s difficult for humans to understand binary numbers. We can convert between binary and denary numbers.
At GCSE, you will only ever work with 8 bit numbers - binary numbers which contain 8 ones or zeros. For example:
0110 1110
As humans we use denary numbers (most of the time) and these have to be stored as binary on a computer - so we have to be able to convert between the two.
To convert back from a denary number to a binary number, we can run the above steps in reverse, subtracting the column headings from the denary number in order.
Unless stated otherwise, most binary numbers you will work with are unsigned. Unsigned binary numbers all represent positive values. Signed numbers can represent positive and negative values. There are three methods of signing binary numbers: Sign Magnitude, One's Complement, and Two's Complement. Sign Magnitude In Sign Magnitude we use the most significant bit (the left most binary digit) to represent if the value is positive or negative. If the left most digit is a 1 it is negative, if it is a 0 then it is positive. An 8 bit Sign Magnitude number can represent values between 127 and -127.
Sign Magnitude is rarely used, if at all, due to a few issues. You cannot easily add two Sign Magnitude numbers together using standard binary addition and you can also end up with positive and negative 0 values:
1000 0000 = negative 0
0000 0000 = positive 0
One's Complement With One's Complement we start with a positive binary number and we flip all of the bits (1s become 0s and 0s become 1s).
Unlike Sign Magnitude, standard binary addition will work on One's Complement numbers. However, there are still positive and negative 0 values:
1111 1111 = negative 0
0000 0000 = positive 0
Two's Complement Two's Complement is the most commonly used method of representing negative numbers on a computer. The process of generating a negative Two's Complement number starts the same was as One's Complement: you take the positive version of your binary number and flip all of the bits (1s become 0s and 0s become 1s). After, you add 1 to the value of the number.
When working with Two's Complement the most significant bit (the left most bit) represents a negative number. In an 8 bit number the most significant bit would represent -128. Two's Complement works with standard binary addition, and does not have a negative and positive 0.
What happens if you need to display a large binary number such as:
1111 1011 1111 1010 0011
Larger binary numbers are hard to remember and hard to write out without making a mistake. Hexadecimal is a number system (base-16) and makes use of 0-9 and A-F. It allows us to work with binary numbers in a more manageable way. Each 4 bits of a binary number can be represented with 1 hexadecimal digit. For example:
1011 = B
Hexadecimal numbers are used commonly when representing colours on web pages.
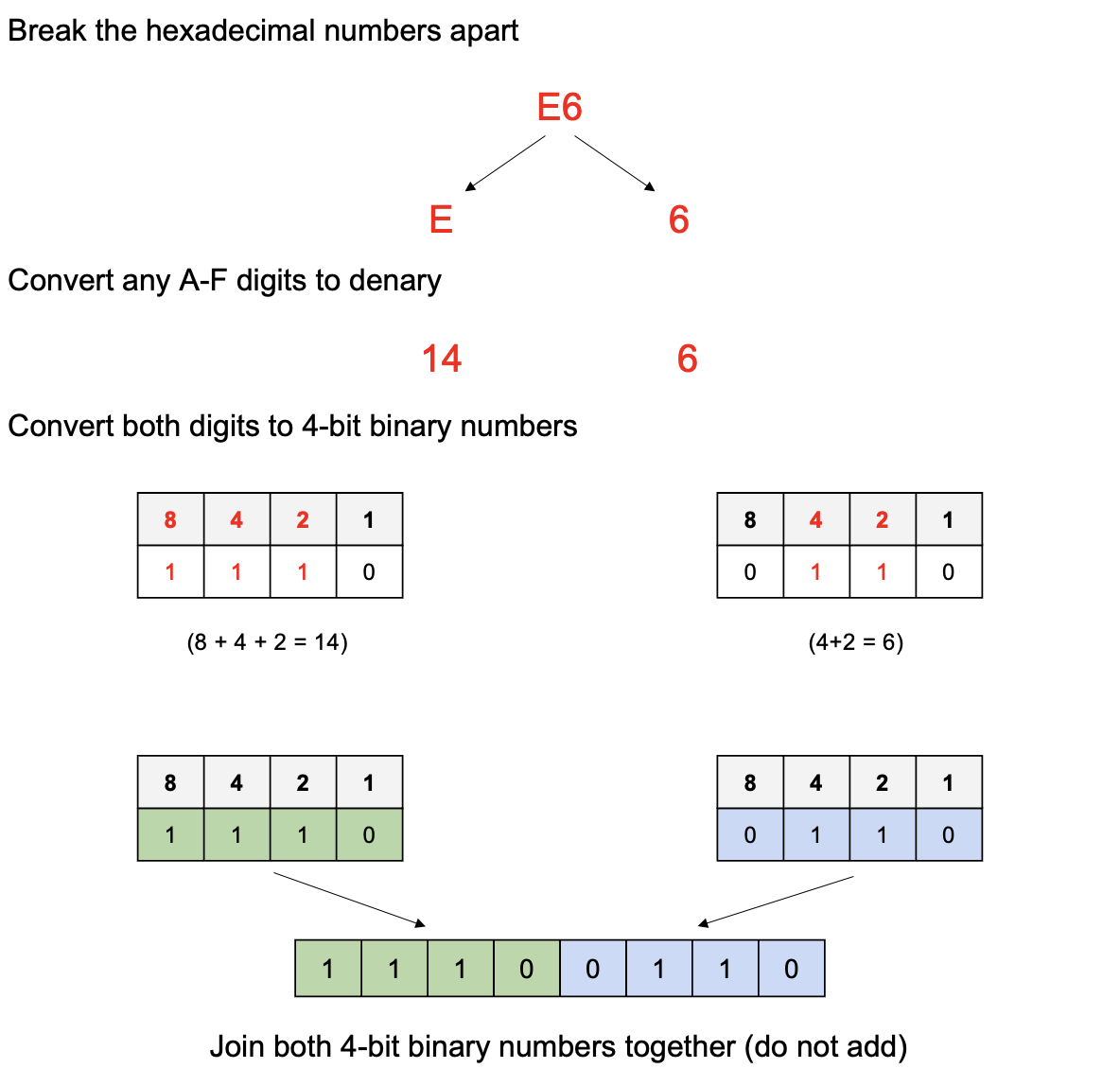
Converting between binary and hexadecimal requires you to understand the basics of converting between binary and denary. At GCSE, you will only ever be asked to convert 8 bit binary numbers (2 digit hexadecimal numbers). Below is how you should convert a two digit hexadecimal number to a 8 bit binary number.
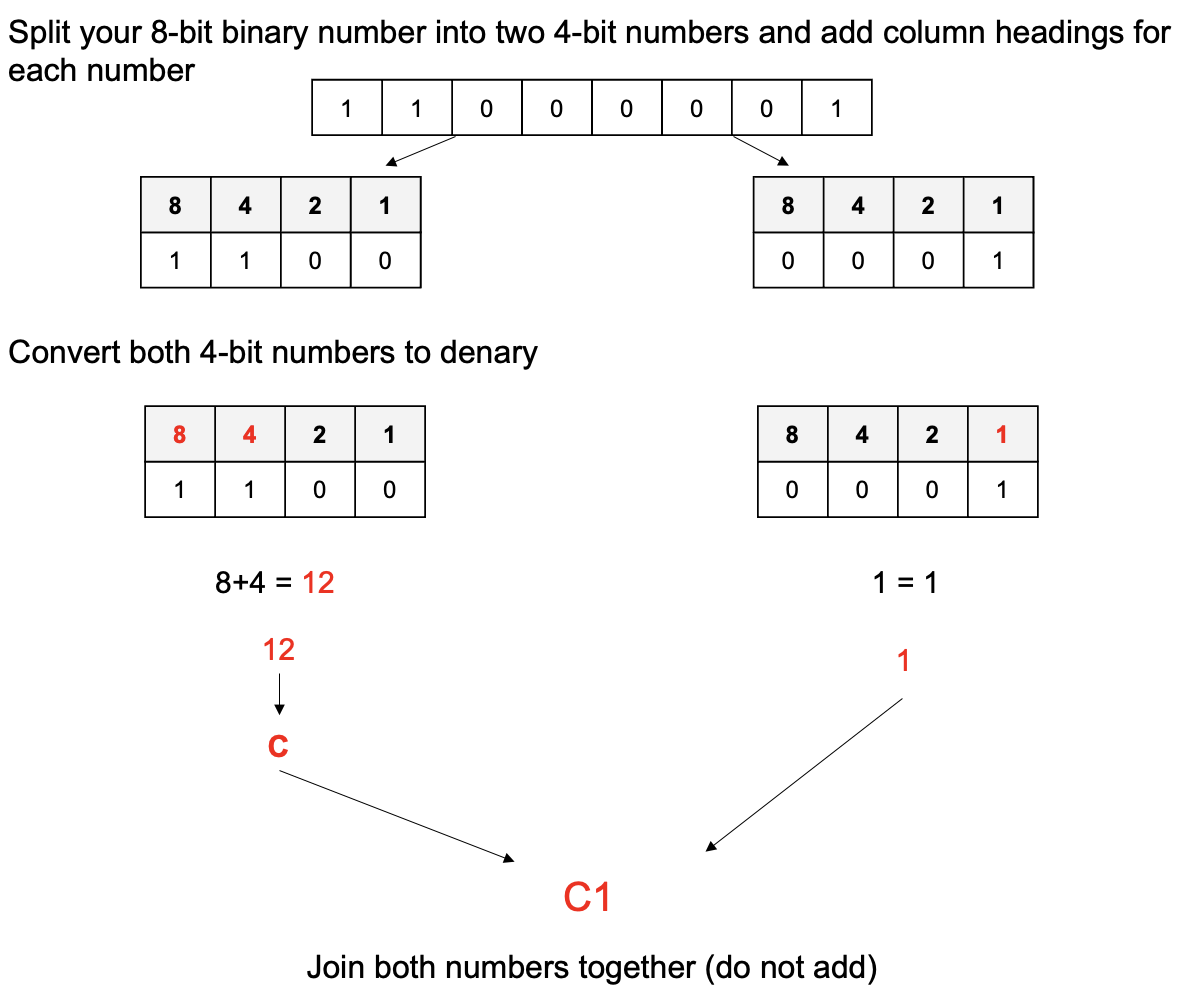
The process is reversed to convert a 8 bit binary number back to a hexadecimal number.
Binary Shifts allow us to multiply binary numbers by moving the position of the 1s.
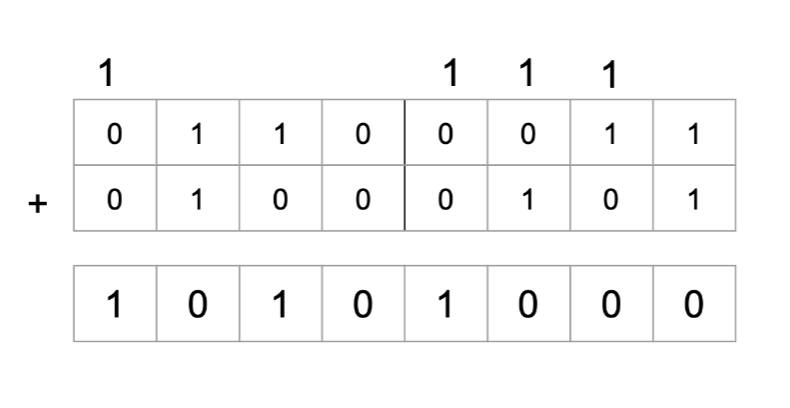
Adding binary numbers works in the same way as denary, just with fewer base numbers! If you follow the 5 basic rules you cannot go wrong:
In the example below we will add together 2 binary numbers:
