Linear search finds the location of an item within an unordered array (collection of data). The algorithm starts at the beginning of the array and checks to see if the first item is the one that is being searched for - if not it moves onto the next item and repeats the process until it finds the desired data.
In terms of performance it can have the best case (finding the desired item first time) and worst case scenario (fining the desired item last).
The major benefit is that it can be ran on an unordered array, however the average case time may be too impractical for larger arrays
The performance limitation of linear search may not be as apparent in a small array, however will become apparent if you are searching for an item in one with millions of entries.
A binary search can only be carried out on an ordered array (numerical or alphabetical) and while more performant is significantly more complex:
The binary seach starts at the middle value, comparing that value to the on that is being searched for. If it is the correct value the search is complete, if not the algorithm determines if the value being searched for is less than or greater than the middle value. The half of the array which the value cannot be in is then discarded along with the middle value. The new middle value is compared and these steps are repeated.
Using a binary search in the example above allowed us to find our desired value in 2 iterations (repeats) of the algorithm. If we were to use a linear search it would have taken 8 iterations! However we could not have ran a binary search on a similar unordered array. Providing an array is in order a binary search will be the most efficent search algorithm available for us to use.
The Bubble Sort is a simple algorithm for ordering the values within an array. However, while it maybe simple, it is not as efficent as other algorithms unless the array it is being applies to meets specific conditions.
Here are the steps the algorithm takes:
The number of passes required increase significantly with the number of items in the array. If the values are in reverse order (which is the worse case scenario) it would take n^2 comparisons. If you had 10 values in reverse order it would take 100 comparisons.
A merge sort breaks down an array into smaller arrays and these smaller arrays are merged in pairs until it is rebuilt into order.
Firstly the array needs to be broken down into individual values. The values are then paired into arrays, and ordered correctly in these new arrays. These arrays are then paired and their values are placed into the correct order. This process is repeated until all the numbers are in order within one array.
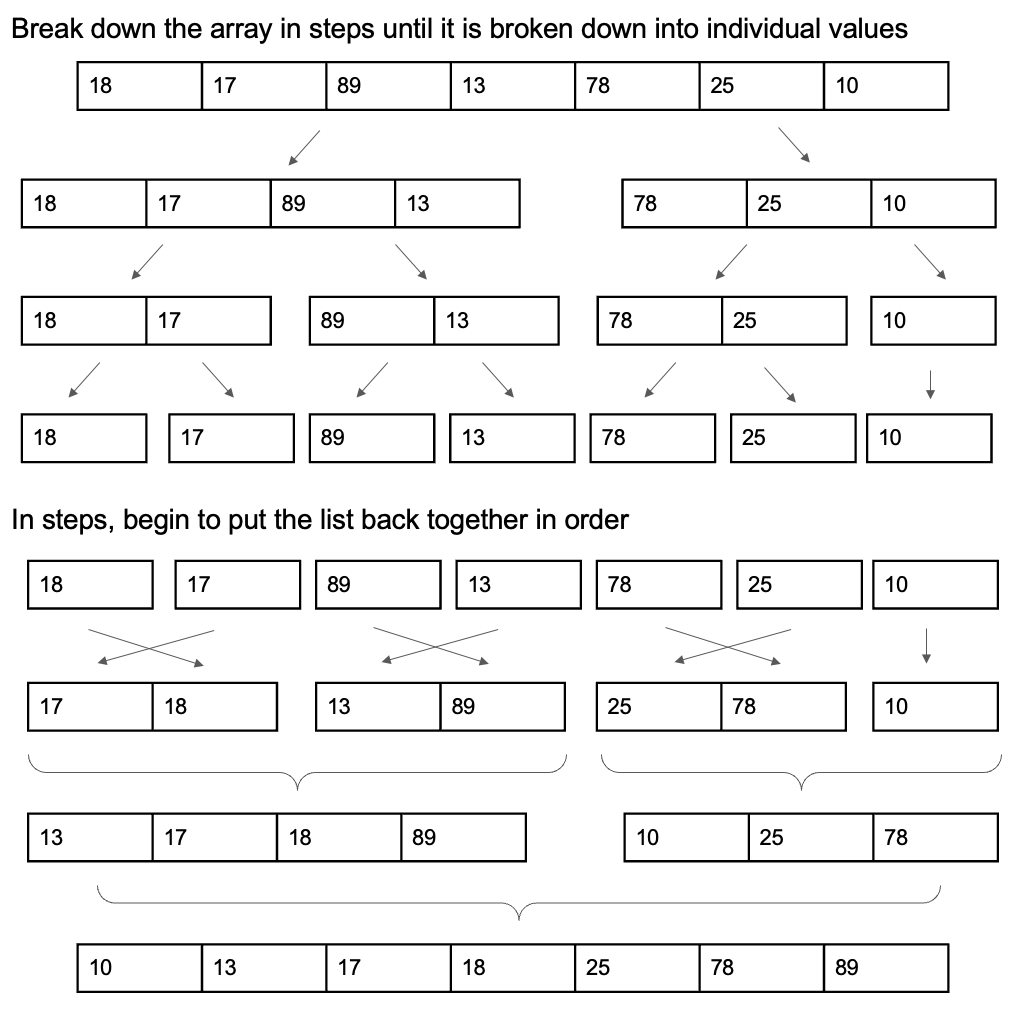
Merge sort is more efficent than a bubble sort when used on larger arrays, however the process is not as simple as with a bubble sort.
Insertion sort progressively sorts an array one value at a time to a new array until it is in order.
Here are the steps the algorithm follows:
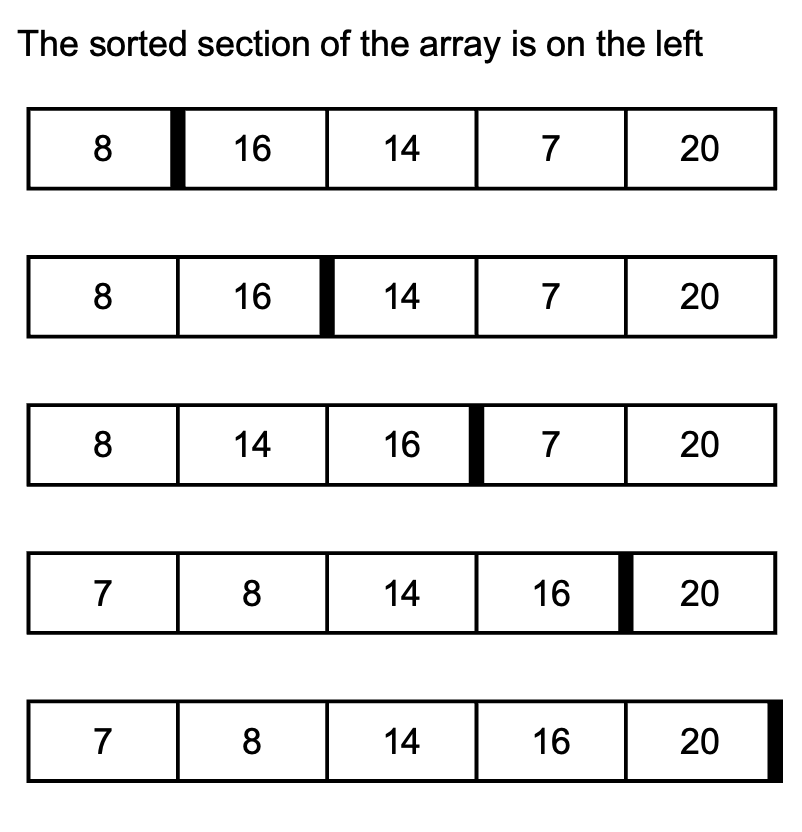
Insertion sort is less efficient with larger lists than merge sort but more efficient than bubble sort. Insertion sort is more memory efficent than bubble sort and merge sort.